|
huutrinon
member
ID 78642
08/21/2014

|
888 về toán học chút chơi...







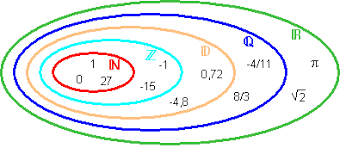
H́nh trên nói về những tập hợp những con số trong toán học...
1) tập hợp N,t.h. số tự nhiên = {0,1,2,3,...}
2) tập hợp Z,t.h. số nguyên = {...,-3,-2,-1,0,1,2,3,...},vv...
---Trong h́nh cũng cho thấy rơ là 'N⊂Z' (N được chứa trong Z,hoặc N là tập hợp con của Z,...)...Vậy xin hỏi các bạn toán học gia,tổng số lượng của những con số trong N,so với tổng số lượng của những con số trong Z như thế nào ? Thí dụ :
---gọi Zs là tổng số lượng của những con số có mặt trong Z
---gọi Ns là tổng số lượng của những con số có mặt trong N, ta có công thức :
--- Zs = 2 Ns ? hay là...
--- Zs = 2,5 Ns ? hay là...
--- Zs = 3 Ns ?, vv....

Alert webmaster - Báo webmaster bài viết vi phạm nội quy
|
 |
|
tuantran20
member
REF: 682280
08/21/2014
|




 

Tôi không hiểu ư HTN lắm
có phải cái này không ?
Z=(5/3)*N
|
 |
|
aka47
member
REF: 682289
08/21/2014
|




 

AK có gọi điện cho GS Ngô Bảo Châu hỏi thử , GS có trả lời là không phải anh TT ạ.
hihii
|
 |
|
huutrinon
member
REF: 682297
08/22/2014
|




 

--- Ừ,khg fải TT à !...Câu hỏi dễ thôi mà...Thí dụ trong tập hợp N,có 'm'(0,1,2,...,m) con số đi(giả thuyết vậy...),th́ câu hỏi là trong tập hợp Z có bao nhiêu con số(2m,3m,4m,vv...) ?
--- C̣n Gs NBChâu trả lời làm sao,sao AKA khg cho các bạn biết luôn... Nói coi gs Châu c̣n nhớ những khái niệm sơ đẳng về tập hợp,về dấu hiệu toán học này khg ?
...Giống giống vầy khg ?...

|
 |
|
rongchoi123
member
REF: 682300
08/22/2014
|




 

Nếu nói theo kiểu VN hoặc Pháp th́ tập hợp N là tập hợp các số tự nhiên:
{0; 1; 2; 3; 4; ............} có vô số số tự nhiên , không thể biêt hết được .
C̣n nói theo kiểu AK (tức theo kiểu Mỹ, v́ AK ở Mỹ) th́ tập hợp N là tập hợp các số tự nhiên {1; 2; 3; ; 4; ........} Cũng là vô số số hạng không thể đếm được, có điều nó chắc chắn là ít hơn kiểu Pháp hay VN 1 số (đó là 0 )
Như vậy nói theo kiểu 1 + 1 = 2. th́ tập hợp Z, tức là tập hợp các số nguyên sẽ có số số hạng gấp đôi tập hợp N thêm 1 (nếu tính theo kiểu AK hay kiểu Mỹ) c̣n tính theo kiểu VN th́ tập hợp Z (các số nguyên) có số lượng các số hạng gấp đôi số lượng các số hạng của N bớt đi 1
|
 |
|
huutrinon
member
REF: 682307
08/22/2014
|




 

--- Chào các nhà toán học,
--- Trước hết,HTN có lời khen ngợi đến RC,có lẽ RC cũng khá về những môn toán,lư,hóa hé ?...Tôi nhớ hồi ḿnh rùm beng về chiện cát ướt,cát khô,cát nào nặng hơn?...Nhớ khg RC?...Kỳ này,RC cũng lại xung fong nữa há? Họ biết, nhưng họ khg dám nói đó RC,v́ fải biết 1 cách chắc chắn,tự tin, th́ mới dám mạnh dạng fát biểu,chớ c̣n ấm ớ như Aka,gọi điện thoại hỏi gs NBChâu, th́ c̣n lâu mới dám trả lời ! Ư là cô nàng là cô giáo dạy toán đó nhe !... Nhưng mà cô giáo ở Mỹ,chắc cũng khg giỏi lắm đâu há ?...V́ như RC nói,ở Mỹ,họ dạy là trong tập hợp N khg có số '0' !?... Ngược ḍng thời gian,khi người Ai Cập fát minh ra con số '0',th́ môn toán học nhờ đó, mà có những bước tiến,nhảy vọt ! Nay người Mỹ lại bỏ con số '0' trong N,có fải là 1 bước lùi vĩ đại khg !?...Hèn chi,cô giáo Aka dạy toán,ở Mỹ, khg được giỏi cho lắm !...
--- Thói thường,người fàm chúng ta lư luận như RC,v́ vấn đề wá giản dị...Theo trực tính,nh́n 2 tập hợp,N & Z,chúng ta thấy liền wan hệ giữa n (những con số hạng trong N)và z(những con số hạng trong Z) là :
-) z = 2n-1 (trừ con số '0' ra...), tức là những con số hạng trong tập hợp Z,đông gắp 2 những con số hạng trong N, - 1,(trừ 1,bỏ con số '0' đi)...V́ tập hợp Z là tập hợp N,cộng với tất cả những con số nguyên Âm...!
--- Nhưng các nhà toán học lại chứng minh rằng : z = n !?...Thật vậy,nếu ta có thể tạo ra 1 wan hệ,1 đối 1,giữa N và Z,th́ dựa theo wan hệ đó,ta suy ra n= z...
Ta có :
--- N --> Z
--- 0 --> 0
--- 1 --> 1
--- 2 -> -1
--- 3 --> 2
--- 4 -> -2,vv... Như vậy N & Z, có số lượng wân bằng nhau,fải khg các bạn ?...
---Bạn nào khg fục,cứ mạnh dạng fát biểu wan điểm toán học của riêng ḿnh !...Sẵn đây,xin cho HTN hỏi cô giáo Aka(luôn cả các nhà toán học khác nữa...),lập luận trên của các nhà toán học có cái ǵ khg ổn khg ? có mâu thuẩn ǵ khg ?...Nếu có,tại sao? Nếu khg,tại sao ?...

|
 |
|
cafekho
member
REF: 682309
08/22/2014
|




 

Nếu dựa trên quan hệ 1 đối 1 để chứng minh Z=N th́ ta cũng có thể chứng minh Z=2N hoặc Z=8N trên quan hệ 1 đối 2 hoặc 1 đối 8.
Vậy với điều kiện (1 đối 1), Z=N mới đúng.
Nếu không có điều kiện 1 đối 1 th́ Z không thể bằng N
mà Z=2N - 1 như anh RC nói.
Chúc vui.
---
|
 |
|
huutrinon
member
REF: 682325
08/22/2014
|




 


---Trong toán học...
-surjection = hàm toàn ánh
-injection = hàm đơn ánh
-bijection = hàm song ánh
---Trường hợp CFK nói 1 đối 2,1 đối 8, là hàm toàn ánh(surjection),trong toán học,người ta khg dùng hàm toàn ánh,và những đặc tính của hàm, để chỉ định số từ số lượng(cardinale) của 1 tập hợp !... Mà fải xử dụng đặc tính của hàm song ánh(bijection) để giải quyết vấn đề(1 đối 1...)
---Dưới đây là 1 đoạn trong 1 tài liệu nói về số lượng của những tập hợp vô tận(infini...) :
[...Commentaire : il y a plusieurs manières de comparer la "taille" d’ensembles. Une première façon est de les comparer au sens de l’inclusion. En ce sens, Q est plus gros que Z, qui est plus gros que N, qui est lui-même plus gros que l’ensemble des entiers pairs. En revanche, au sens des cardinaux, c’est à dire au sens où ils peuvent être mis en bijection, ces ensembles ont la même “taille". C’est surprenant, mais c’est comme ça. Ceci vu, de nombreuses questions se posent. En particulier, tous les ensembles infinis peuvent-ils être mis en bijection avec N? La réponse est non : on peut montrer qu’il n’y a pas d’ensembles infinis plus petits que N, mais il y a des ensembles plus gros. L’ensemble des réels R, notamment, est vraiment plus gros que N...]
--- Ở đây,họ nói về những tập hợp N,Z,Q,R,......Trừ R ra,những tập hợp vừa kể đều có số từ số lượng(cardinale) bằng nhau hết...Và những tập hợp Z,Q,R đều chứa tập hợp N...
--- Và những khái niệm tập hợp,chứa đựng,tập hợp con,số từ số lượng,vv...nói trên khg có mâu thuẩn ǵ với nhau,v́ chúng ta đang nói tới những tập hợp vô hạn(infini...)... Fải chi chúng ta nói đến những tập hợp hữu hạn (fini...),th́ ta lại có những định luật có hơi khác...
|
 |
|
rongchoi123
member
REF: 682326
08/22/2014
|




 

Theo quan hệ bao hàm th́ tập hợp N nằm trong tập hợp Z
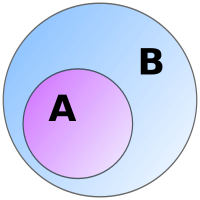
H́nh vẽ của các nhà toán học đă minh họa cho học sinh. Thế mà họ lại chứng minh rằng Z = N hay nói chính xác số phần tử của Z = số phần tử của N. Có mâu thuẫn không?
Theo rongchoi cũng không mâu thuẫn lắm v́ tập A chứa trong tập hợp B th́ có thể có trường hợp tập A = tập B. V́ theo định nghĩa toán học: Một tập hợp chứa trong chính nó _ B chứa trong B hoặc A chứa trong A. Tương tự, N chứa trong N, Z chứa trong Z,.... (dù rằng N chứa trong Z và Z chứa trong Q và Q lại chứa trong R).
Nếu chứng minh được số phần tử của Z và N bằng nhau th́ cũng không có chi lạ. V́ cả hai tập hợp này đều có số phần tử không đếm được, vô số phần tử. Mà cái ǵ ở vô cực, ở cơi thượng giới th́ đối với những kẻ phàm trần như ta chúng là siêu đẳng như nhau cả.
Cái này cũng như thằng bé học lớp 1 th́ thấy không có ǵ khác biệt giữa ông cử nhân và ông tiến sĩ.
|
 |
|
huutrinon
member
REF: 682327
08/22/2014
|




 

--- Hay ! Lại fải khen RC,v́ giải thích giản dị, dễ hiểu 1 đề tài hơi khó tŕnh bày...Ưu điểm này,OT cũng có đó...Nếu OT chịu nhảy vô,tui tin chắc OT giải thích nghe cũng bùi tai lắm...

|
 |
|
aka47
member
REF: 682337
08/22/2014
|




 

Vậy là anh HTN không biết anh RC rùi.
Anh RC và ông Ngô Bảo Châu là anh em thúc bá , anh RC vai lớn hơn đó anh.
OT vô cũng suưt soa thôi chứ hổng có lên tiếng đâu.
hihii
|
 |
|
cafekho
member
REF: 682341
08/22/2014
|




 

Anh HTN nhắc về hàm toàn ánh hay song ánh th́ Cf mới từ từ nhớ lại mấy khái niệm này nhưng vẫn chưa t́m thấy tại sao lại không áp dụng vào tập hợp số được. Trên kia là cafe chỉ dùng logic thông thường để giải thích thôi.
Để t́m hiểu thêm hén.
Cf cũng cảm ơn anh HTN đă khơi dậy lại được ư thức học toán của ḿnh.
Về tập hợp hữu hạn và vô hạn ḿnh cũng có một vài bài toán hay, sẽ đề cập khi sử dụng máy tính (v́ giờ đang dùng đt ngu ;))
Happy
---
|
 |
|
huutrinon
member
REF: 682351
08/23/2014
|




 

--- @ Aka,
Anh HTN khg biết liên hệ giửa RC và NBChâu,trong gia fả của họ ra làm sao! Aka nói ra, anh mới biết... À mà sẵn dịp,HTN trả lời luôn cho RC,khg fải bên Mỹ họ quy định là N = {1,2,3,...,∞} ! mà khi cần, họ quy định viết như sau :
N - {0} = N*...
--- @ CFK,
[...nhưng vẫn chưa t́m thấy tại sao lại không áp dụng vào tập hợp số được...],trích CFK...
...Họ đưa ra khái niệm về hàm toàn ánh,hàm đơn ánh, để rồi đi đến kết luận là :
--- hàm toàn ánh + hàm đơn ánh = hàm song ánh...
Và rồi nêu ra những đặc tính của hàm song ánh mà khai triển đến những khái niệm,những đặc tính của những con số,của những tập hợp N,Z,Q,R,C,...... Lấy ví dụ,ta lấy 1 ánh xạ toàn ánh f(x)=y,(application surjective), 1 đối 2,1 đối 8,kiểu như CFK thí dụ trên...ta có :
--- f(x1) = y1, f(x2) = y1 (2 đối 1)
và ngay trong ánh xạ f(x) =y,ta cũng có thể có (khg có mâu thuẫn nào hết!...):
--- f(x3)=y2,f(x4)=y2,f(x5)=y2,f(x6)=y2,f(x7)=y2,f(x8)=y2,f(x9)=y2,f(x10)=y2 (8 đối 1)
thử hỏi,với 1 tương quan toàn ánh như vậy(hàm đa trị),làm sao ta có thể thiết lập những định luật ǵ? về bất cứ đề tài ǵ,trong toán học !...Chỉ có ánh xạ song ánh (hàm đơn trị) là cho fép ta thiết lập 1 quan hệ khg bừa băi,giữa đặc tính của hàm số và những quy luật trong toán học...(tui nói mà tui c̣n khg hiểu,đố ai hiểu nổi !)
Một đoạn tài liệu để tham khảo :
[---Toàn ánh, đơn ánh và song ánh

Toàn ánh là ánh xạ từ X vào Y trong đó ảnh của X là toàn bộ tập hợp Y. Khi đó người ta cũng gọi f là ánh xạ từ X lên Y : f(X)=Y
hay

Đơn ánh là ánh xạ khi các phần tử khác nhau của X cho các ảnh khác nhau trong Y.Đơn ánh c̣n được gọi là ánh xạ 1-1 v́ tính chất này.

hay

Song ánh là ánh xạ vừa là đơn ánh, vừa là toàn ánh. Song ánh vừa là ánh xạ 1-1 và vừa là ánh xạ "onto" (từ X lên Y)...]
|
 |
|
aka47
member
REF: 682352
08/23/2014
|




 

Anh HTN.
Em nghe nói ở VN có rất nhiều người tài giỏi , tiến sĩ Toán , Vật lư , Hóa học và có cả ngàn ngàn những nhà khoa học.
Nhưng hầu hết (hầu hết chứ ko phải toàn bộ) họ chỉ giỏi trên lư thuyết , c̣n khi thật sự thực hành th́ họ lại chịu thua.
Vậy là sao bớ anh Hai?
hihii
|
 |
|
huutrinon
member
REF: 682357
08/23/2014
|




 

--- Bên Đông Fương,có triết lư Kinh Dịch (tương tự Đạo Lăo,Khổng Tử th́ khg fải Lăo Tử nhe...),triết lư Đạo Fật(nói cho chính xác,tư tưởng Đạo Fật khg fải là 1 triết lư,nó vượt lên trên Triết Lư...)... Bên Tây Fương,có tư tưởng Triết,Lư Luận của các môn khoa học thực tiễn,dẫn đầu là các môn : Toán,Lư,Hóa,...
--- Toán học là 1 môn có lư luận vững chắc,logic...nhưng trừu tượng...dựa trên nền móng của Tư Tưởng...Thuộc về lănh vực Ư Thức của nhà Fật(6 Thức : Mắt,Tai,Mũi,Lưỡi,Thân,Ư...). Nên Aka nói về Lư thuyết của Toán Học là như... khg có nói ǵ hết ! Toán học chỉ là 1 mớ những ư tưởng,lư thuyết mà thôi !...Những ư tưởng,lư thuyết đó được sáng tạo,vẽ ra, dựa trên 1 lập luận logic,hợp lư...Nên các nhà toán học đều là những nhà chuyên môn về lănh vực Ư Tưởng,về lư thuyết vậy...
--- C̣n khi em nói bên VN,có nhiều nhà khoa học nổi tiếng,th́ anh HTN khg biết chính xác về vụ việc này ! Có lẽ chỉ là lời đồn thôi em à ! Nói chiện fiếm,888 chơi, bên Trời Đông,nói về những nhà Tư Tưởng nổi trội về những môn khoa học thực nghiệm(sciences expérimentales) Tây Fương,th́ khg có nước nào sáng chói hết,ngay cả Tàu !... Duy có về Toán Học,v́ là 1 môn rất trừu tượng như chúng ta đă nói ở trên, th́ có Ấn Độ,Iran,...v́ đó là những nơi fát xuất ra những nền văn minh cổ kính(người Ấn Độ nổi tiếng về lănh vực ư tưởng trừu tượng...,nên họ giỏi Toán khg fải là chiện lạ !)
--- Nền khoa học thực nghiệm Tây Fương gồm nhiều môn học : Toán,Lư,Hóa,Y khoa,Khoa Học nhân Bản,vv... Nhưng đứng đầu nền khoa học đó,là môn Toán Học...Toán Học chi fối hầu hết các bộ môn khác...Aka làm trong ngành giáo dục,để ư em sẽ thấy,cho đến Tú Tài(Tốt Nghiệp Phổ Thông...),tất cả các ban đều bắt buộc fải học Toán,chỉ khác nhau ở mức độ chuyên nhiều hay chuyên ít mà thôi !...

|
 |
|
aka47
member
REF: 682358
08/23/2014
|




 

Bái phục anh HTN.
Anh lư luận thật chính xác và vững chắc.
Anh không làm giáo sư để hướng dẫn SVHS Đại Học thật là uổng.
Thích anh quá.
hihii
|
 |
|
rongchoi123
member
REF: 682367
08/23/2014
|




 

huutrinon có lẽ hơi bị nhầm chăng?
Ở Mỹ qui định tập hợp các số tự nhiên N không có số 0
Ở VN (theo trường phái của Pháp) qui định số tự nhiên N có số không. Nhưng ở VN và Pháp có qui đinh N* là tập hợp các số tự nhiên không có 0. C̣n ở Mỹ mặc nhiên N là không có 0. Người Mỹ lư luận rằng trong tự nhiên không tồn tại 0. Cũng vậy, không ai nói tôi có 0 tiền, tôi có 0 cái nhà cả, nói vậy không tự nhiên. Người ta chỉ nói tôi không có tiền hay tôi không có nhà. Tương tự, trong một khu vườn không ai nói có không cây táo cả mà người ta nói khu vườn không có cây táo.
Do đó, khi thi toán quốc tế các bài toán về số tự nhiên thường người ta nêu rất rơ điều kiện là tập hợp đó có 0 hay không có 0 để học sinh làm. Hoặc người ta nói rơ hơn "cho tập hợp các số tự nhiên khác 0", hoặc "cho tập hợp các số nguyên dương". (số nguyên dương là số nguyên không âm và khác 0). Hoặc người ta nói "cho tập hợp các số tự nhiên kể cả 0"Dĩ nhiên , chú thích bằng tiếng Anh.
Đây là một đoạn văn của người Mỹ:
The term "natural number" refers either to a member of the set of positive integers 1, 2, 3, ... or to the set of nonnegative integers 0, 1, 2, 3, ... .
Thuật ngữ "số tự nhiên" nói đến hoặc là các phần tử của tập hợp các số nguyên dương 1, 2, 3,.....
Regrettably, there seems to be no general agreement about whether to include 0 in the set of natural numbers. In fact, Ribenboim states "Let P be a set of natural numbers; whenever convenient, it may be assumed that 0 in P."
Đáng tiếc là dường như không có sự thống nhất chung về việc có kể thêm 0 vào tập hợp số tự nhiên hay không. Thực sự, Ribenboin (một nhà toán học nổi tiếng) phát biểu rằng "Cho P là tập hợp các số tự nhiên; khi cần thiết, ta có thể giả định rằng P có chứa 0"
|
 |
|
huutrinon
member
REF: 682481
08/25/2014
|




 

--- HTN khg bị lầm đâu,RC !...Đơn giản là HTN khg hề biết tới vụ này, nghe RC nói mới biết đây thôi,vụ N = {1,2,3,...}...V́ chắc HTN học theo hệ Fáp,nên hồi nào tới giờ chỉ biết N là tập hợp N = {0,1,2,3,...}. HTN có tham khảo tài liệu,khg fải chỉ bên Mỹ thôi đâu,mà ngay cả bên Âu Châu,cũng có nhiều học giả cho là trong tập hợp N, khg có con số {0}...
Nhưng HTN cho rằng,trong N,khg có số '0',tạo cho ta nhiều sơ sót...
1) Theo tiên đề của Peano(nhà toán học Ư...),trong tập hợp N có dấu hiệu (symbole) '0'...Họ quy định ghi khái niệm con số 0 bằng '0' (khg ai cấm họ ghi con số 0 bằng 'ζ',hay 'ῆ',hay 'τ',vv...nhưng họ đă quy định như thế !)
2) Fải đặt lại các fép toán số học,trong tập hợp N :
--- a trong N,a - a = ?, nếu khg có số '0' !
3) Nếu trong N khg con số '0' th́ ta khg có định luật này trong fép nhân (x) :
--- ax0 = 0xa = 0...cũng như,ta sẽ khg có định luật dưới đây,trong fép chia :
--- a/0 : vô nghĩa !...(nên nhớ fần tử '2/1',vv... thuộc về N)
--- Nhưng may mắn thay,toán học khg ngừng ở tập họp N,nên có lẽ vấn đề có hay khg có con số '0' trong N, khg là vấn đề lớn với các nhà toán học,nên mới có những tiên đề thành lập tập hợp N,bắt đầu bằng số '1',thay v́ số '0' !
--- Cũng nên nhớ,con số '0',xuất hiện từ lâu đời lắm,trước tiên đề của Peano...
Dưới đây là 1 đoạn ngắn,nói về lịch sử của con số '0'...
[...En 628, le savant Brahmagupta dans son traité " Brahma-sphutasiddhârta ", définit le zéro comme la soustraction d'un nombre par lui-même: a – a = 0 et il en décrit les propriétés:
a + 0 = a
a – 0 = a
a . 0 = 0
Il va jusqu'à affirmer que la division par zéro est une définition de l'infini.
Le zéro apparut vraiment vers 870 dans des écrits hindous.
* À l'origine le mot hindous " sunya " ou " shûnya " signifie vide, néant.
* Au IXe siècle, les Indiens l'utilisaient dans leur système numérique de position.
* Au 12e siècle, le zéro est représenté par un point, le bindu.
Mayas:
Au 3e siècle, trois siècles avant les Indiens, les Mayas avaient développé un système de numération très poussé, basé sur l'art du calendrier et de l'astronomie.
Ils avaient, eux aussi, inventé une numération de position à base 20 et comportant le zéro...]
--- Đại khái là : vào năm 628,nhà bác học Brahmagupta...
--- Vào thế kỷ 9,người Ấn Độ,,,
--- Vào thế kỷ 12,số '0' được biểu thị bằng 1 dấu chấm ('.')...
--- Vào thế kỷ 3,3 thế kỷ trước người Ấn Độ,người Maya...
--- Tóm lại,con số '0' đă được fát minh từ rất lâu đời,và Peano đă thành lập tập hợp N(Peano là người đầu tiên đưa ra những 'tiên đề Peano' về tập hợp N...), bắt đầu bằng con số '0'... Thật ra tôi khg hiểu, trường fái lập ra tập hợp N,bắt đầu bằng con số '1'(khg có số '0'), có những lư do ǵ chánh đáng ?
--- Trên đây là 888 để 888 chơi về tập hợp N,có hoặc khg có con số '0', chớ RC hoàn toàn nói sự thật,khi anh ta nói là bên Mỹ họ thành lập tập hợp N ={1,2,3....}
|
 |
|
cafekho
member
REF: 682668
08/28/2014
|




 

2 bạn "trẻ" HTN và RC nói chuyện toán học nghe rất hay.
Cafe vẫn không ngừng t́m kiếm tài liệu để chứng minh điều anh HTN nói là đúng/sai đó. :)
Về bài toán tập hợp hữu hạn th́ theo trí nhớ là có mà không biết để ở đâu rùi, kiếm quài chưa ra, để khi nào kiếm ra sẽ dán lên nha anh HTN.
:)
---
88 nhé
RC hoàn toàn không có quan hệ ǵ với GS Ngô Bảo Châu đâu, mấy bạn lộn rồi, chỉ có một người có quan hệ với GS Ngô Bảo Châu mà Cafe từng nghe kể đó là Ngô Bảo.. Gia.
Ngô Bảo Gia là con trai "rơi" của GS Ngô Bảo Châu tại v́ giáo sư bữa đó đi chơi xài đúng cái Bao Giả nên đặt tên cháu là Ngô Gia Bảo, nhưng mà không được đúng họ Ngô Bảo nên đổi thành Ngô Bảo ..Gia.
Bảo Gia - Bao Giả thật là ư nghĩa và hay phải không các bạn. Trí tuệ của GS thật là siêu việt.
Tin hay không kệ mẹ nhé, các mẹ ui.
(dạo này chơi webtretho nh́u quá, thông củm)
--
|
 |
|
rongchoi123
member
REF: 682695
08/28/2014
|




 

bác huutrinon nói đúng. huutrinon không lầm mà không biết thôi. V́ người Mỹ làm ǵ có tập N*, cái này là của người Pháp, người Việt . Người Mỹ mặc nhiên N là không có 0 rồi. HỌ có lư của họ chứ không vô lư đâu. Nói chung, đó là ư kiến riêng của họ, các nhà toán học khác tôn trọng cũng như họ tôn trọng ư kiến của các nhà toán học người Pháp là N th́ phải có 0 .
Nói về toán hữu hạn, vô hạn th́ đi quá xa tŕnh độ c̣i về toán của rongchoi rồi. Thời học sinh đă xa, bây giờ c̣n nhớ bài toán vô hạn đơn giản thế này.
Chứng minh 0,99999999999...... (vô số số 9) bằng 1.
Có thể chứng minh bằng cách của tiểu học hoặc cách của lớp 11
Từ đó chứng minh được:
1/9 = 0,111111111111111111111.......(số 1 kéo dài vô hạn)
2/9 = 0,222222222222222222222222222.......
3/9 = 0,333333333333...........
4/9 = 0,44444444444444444444444.......
5/9 = 0,55555555555555555...........
6/9 = 0,666666666666666...............
7/9 = 0,7777777777777777777.........
8/9 =0,88888888888888888888888888........
9/9 = 0,999999999999999........ = 1
Cái này th́ bác huutrinon chắc chắn là chứng minh được.
|
 |
|
phuongtimhoang
member
REF: 682700
08/28/2014
|




 

Thú thật là hồi đó ,đến giờ toán học,
th́ chỉ có phe nam sinh là hăng say chậy
tới chậy lui lên bảng cùng giáo sư thôi !
C̣n phe nữ sinh th́ được tự do ngồi ăn vụng lén..
Có lẽ nhờ vậy mà giờ PTH nh́n nó như mù nh́n voi....hihhiii ,
Phục các ông anh quá đi !
|
 |
|
huutrinon
member
REF: 682703
08/28/2014
|




 

--- @ CFK,
--- CFK lại lộn xộn nữa rồi ! Ở trên đă lầm lẫn hàm toàn ánh với hàm song ánh... Giờ lại lộn xộn giữa NBChâu với Cù Huy Hà Vũ !... Ngô Gia Bảo đâu có dính líu ǵ với NBChâu ! Cùng lắm,CFK lật gia fả của Ngô Gia Bảo ra coi có ăn nhậu ǵ với Ngô Gia Tự khg(đường NGTự ở ngă 7 Lư Thái Tổ,Lê Hồng Fong...) ?
--- C̣n người xài bao giả là Cù Huy Hà Vũ,chớ NBChâu, muốn chứng minh đường thẳng giao với mặt phẳng,hay ellipse ǵ ǵ đó...,đâu cần tới tiên đề bao cao su ? Fải hông nè ?
--- @ RC,
[...Cái này th́ bác huutrinon chắc chắn là chứng minh được...], trích RC...
Lại sai rồi...những con số đó thuộc tập hợp Q hay R ǵ đó...HTN chỉ có thể t́m tài liệu chứng minh mấy vụ đó cho các bạn thảm khảo,chớ HTN làm ǵ mà chứng minh được !... Tôi c̣n nhớ,hồi c̣n học ở trường,khi thầy giảng tới mấy vụ đó,tôi c̣n khg hiểu hết,lấy đâu ra mà chứng minh bây giờ đây !...
 
|
 |
|
huutrinon
member
REF: 682705
08/28/2014
|




 


---Post lên h́nh trên làm tiền đề cho góp ư của ChânChờiTím(PTH)... Họ nói bộ óc ta chia làm 2 bên : bên trái + bên fải... Theo h́nh trên, fần bên trái bộ óc thuộc về lănh vực ư nghĩ,ư tưởng : logic,phân tích,kỹ thuật...đàn ông con trai,thường hay fát triển fần này... Fần bên fải bộ óc thuộc về lănh vực trực giác : toàn thể,tổng hợp,tức thời...đàn bà con gái,thường hay fát triển fần này...
--- Thí dụ cụ thể để chứng minh thuyết trên : CFK có bồ đẹp lắm,mà lại thích đi ăn vụng...Xong rồi, khi đi gặp bạn gái,anh ta lên sẵn 1 dự án để nói dối khg có lấy được 1 chút sơ hở nào hết (v́ anh này fát triển fần óc bên logic hết ư luôn...) ! Nhưng khi gặp bạn gái,và tŕnh bày đề án,th́ cô nàng nói ngắn gọn : nếu anh c̣n tới lui với con nhỏ đó,th́ kể như chấm dứt giữa tôi với anh (cô này fát triển fần trực tính của bộ óc...làm ǵ wa mặt được cô ta?...)! Khg tin,các bạn hỏi CFK đi...
--- Vậy đàn ông,đàn bà, con trai,con gái, ai hơn ai ?...
|
 |
|
rongchoi123
member
REF: 682848
08/30/2014
|




 

Hôm nay rănh vào lại topic cũ , thấy huutrinon bảo là không chứng minh được cũng lạ? Đă tám về toán học cỡ này th́ mấy cái nhỏ đó làm được chứ?
Sau đây là một cách dễ ợt, tiểu học cũng hiểu khỏi cần dùng giới hạn với đạo hàm làm ǵ
Đặt A = 0,999999999......(số 9 kéo dài vô tận)
Vậy th́ 10.A = 9,9999999..........
Do đó: 10A - A = 9
Mà 10A - A = 9A
nên 9A = 9 suy ra A = 1, tức là 0,99999.......... = 1
|
 |
|
huutrinon
member
REF: 682887
08/31/2014
|




 

--- 'Logic toán học khg fải là vấn đề quan điểm'...Tây,họ hay rêu rao câu nói đó...Mà đúng thật ! Chứng minh trên của RC,đố ai mà t́m ra được chỗ sơ hở !?...
Nhưng HTN nhớ mài mại về 1 khái niệm khác,RC à ! Cái ǵ như những số thực (nombres réels)...

--- Họ đưa vô những khái niệm về 'classe' (tập hợp, lớp ?),và chứng minh rằng mỗi 1 con số đều có thể lập 1 wan hệ với 1 'classe'. Và cứ thế,họ chứng minh những số thực (nombres réels) khg thuộc về tập hợp Q (HTN mường tượng về những khái niệm đó,nên trả lời lạc đề, với câu hỏi của RC về chứng minh trên! )!...
--- Dù sao đi nữa,chứng minh trên của RC,giản dị,dễ hiểu và rất thuyết fục...
|
1
|
|
|
Kí hiệu:
 :
trang cá nhân :
trang cá nhân  :chủ
để đă đăng :chủ
để đă đăng
 :
gởi thư :
gởi thư
 :
thay đổi bài :
thay đổi bài
 :ư kiến :ư kiến |
|
|
|
|
|



